Electromagnetic Wave Analysis: Unraveling the Genius of John Mighton

John Mighton, a name that might strike unfamiliar to many, yet he has made groundbreaking contributions to the field of electromagnetic wave analysis. This article will delve into the fascinating world of electromagnetic waves and shed light on the genius mind behind their analysis - John Mighton.

Understanding Electromagnetic Waves

Electromagnetic waves are everywhere around us, although often unseen. From radio signals to light waves to X-rays, they play a crucial role in our modern lives. These waves are a combination of electric and magnetic fields oscillating at perpendicular angles, propagating through space. The study of electromagnetic waves involves understanding their properties, behavior, and applications.

The Pioneering Work of John Mighton

John Mighton, a Canadian mathematician, playwright, and founder of JUMP Math, has taken a unique approach to analyze electromagnetic waves. His groundbreaking research and discoveries have opened up new possibilities for our understanding and utilization of these waves.

Electromagnetic wave analysis

by John Mighton([Print Replica] Kindle Edition)

4.8 out of 5

Language	:	English
File size	:	3294 KB
Screen Reader	:	Supported
Print length	:	275 pages
X-Ray for textbooks	:	Enabled

FREE

The Importance of Wave Analysis

Wave analysis is essential for a wide range of fields, including communications, medicine, remote sensing, and more. By understanding the behavior of waves, we can develop better technologies, improve data transmission, and gain insights into the world around us.

Mighton's Contributions

John Mighton's work in electromagnetic wave analysis has revolutionized how scientists and engineers approach the subject. He has developed advanced mathematical models and algorithms to analyze complex wave patterns, uncovering hidden patterns and relationships that were previously unknown.

One of Mighton's key contributions is the development of a new wave analysis technique called the "Spectral Decomposition Method." This method allows for the decomposition of complex waveforms into their constituent frequencies, enabling a detailed understanding of their characteristics. The spectral decomposition method has found applications in fields such as signal processing, image analysis, and medical diagnostics.

Applications and Impact

The impact of John Mighton's work in electromagnetic wave analysis is far-reaching. It has paved the way for advancements in various fields, including:

• Communication Technology: By understanding wave propagation characteristics, researchers have improved wireless communication systems, leading to better signal quality and increased data transmission rates.
• Medical Imaging: Spectral decomposition techniques have enhanced the accuracy and efficiency of medical imaging technologies such as MRI and ultrasound. This has resulted in more precise diagnoses and improved patient outcomes.
• Remote Sensing: The analysis of electromagnetic waves has enabled scientists to gather valuable data about Earth's atmosphere, oceans, and land surfaces. This information aids in climate studies, weather forecasting, and environmental monitoring.
• Wireless Power Transfer: Mighton's research has fostered advancements in wireless power transfer technologies, allowing for efficient charging of devices without the need for physical connections.

The Genius Behind the Waves

John Mighton's brilliance extends beyond his contributions to electromagnetic wave analysis. He has honed his understanding of wave behavior through rigorous experimentation and mathematical modeling. His innovative thinking and analytical skills have allowed him to make significant breakthroughs in this field.

Aside from his mastery of wave analysis, Mighton is also well-known for his contributions to education. He founded JUMP Math, an organization focused on improving mathematical skills among students. His dedication to education and his ability to make complex concepts accessible have earned him numerous accolades and recognition.

Electromagnetic wave analysis is a fascinating field that holds immense importance in our technologically advanced world. John Mighton's contributions and insights have helped unravel the mysteries of these waves, leading to advancements in various industries. His genius and passion continue to inspire fellow scientists, engineers, and educators.

So, the next time you use your smartphone, undergo a medical scan, or hear about innovations in wireless technology, remember the name John Mighton - the brilliant mind behind electromagnetic wave analysis.

Electromagnetic wave analysis

by John Mighton([Print Replica] Kindle Edition)

4.8 out of 5

Language	:	English
File size	:	3294 KB
Screen Reader	:	Supported
Print length	:	275 pages
X-Ray for textbooks	:	Enabled

FREE

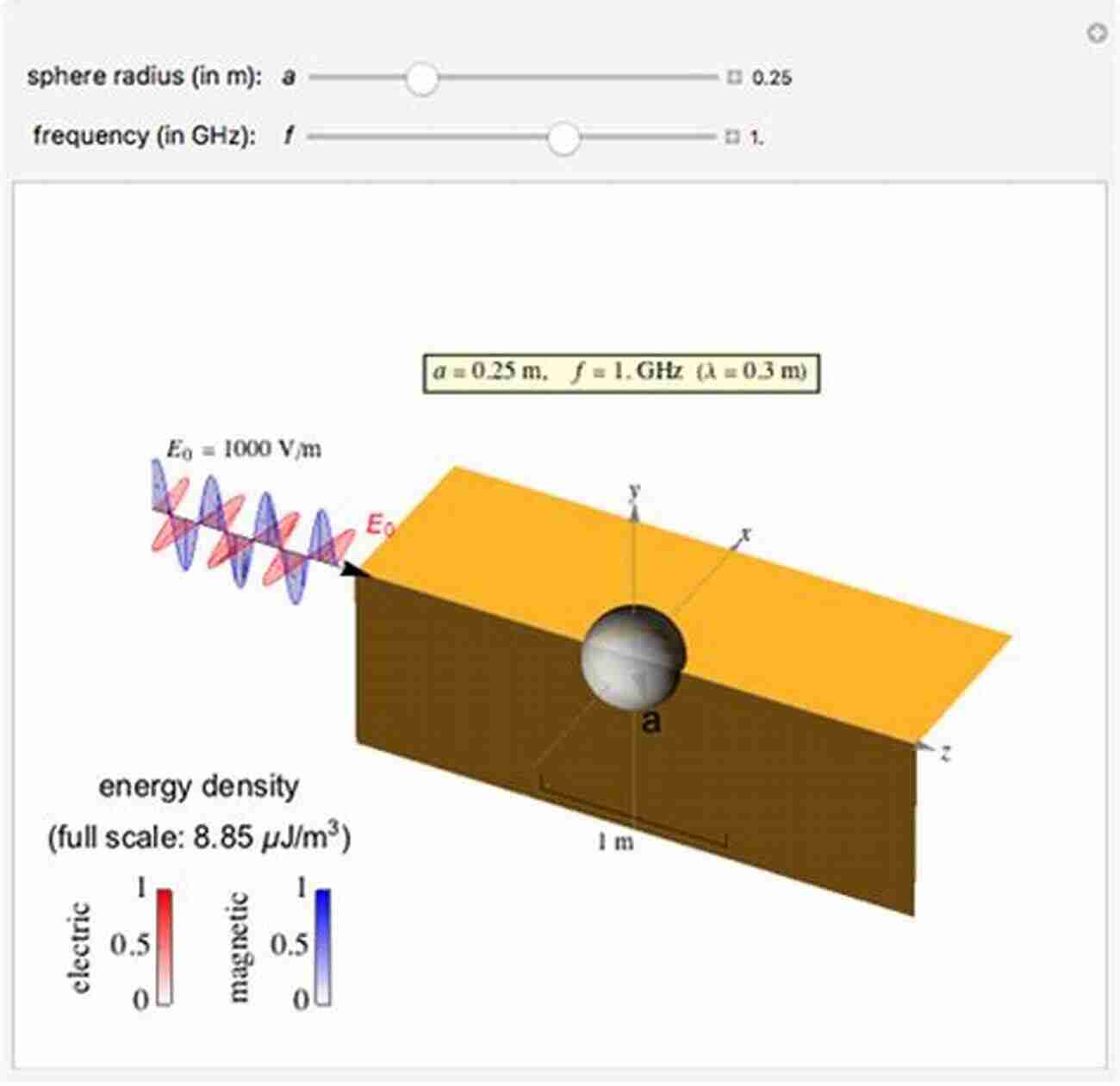
In this book, we start with radiation from a source and explain the equivalent theorem for electromagnetic waves. After that, the equivalent mathematical analysis model is explained in relation to the analysis of differential equations. Specifically, the solution of the electromagnetic scattering problem is explained in terms of structures conforming to the orthogonal coordinate system. In particular, the equivalence theorem is an important theorem which guarantees that the electromagnetic field at a point of interest should consider only the information of the region of the point of interest (the sources, the value at the boundary, the medium constant, etc.),but in many cases, the electromagnetic field problem is solved without knowing the equivalence theorem.
The goal of this book is to understand the physical phenomena of field problems by using knowledge of mathematics. Specifically, the differential equations are solved by using the knowledge of Fourier series, Fourier transform, complex functions and so on, in addition to physical conditions. In recent years, there are many cases in which the field boundary value problems are solved by general-purpose field simulators, even for complex shapes. However, it is difficult to understand the essence and universality of physical phenomena by only simulating the field distribution in animation. Returning to the few canonical field problems treated in this book, we believe that understanding the universal behavior of wave phenomena and the equivalent relationship between analytical and real models are useful for understanding and improving the accuracy of approximate solutions of complex phenomena.

Jiro Hirokawa was born in Tokyo in 1965. He received the doctoral degree in electrical and electronic engineering from Tokyo Institute of Technology in 1994. He is currently a professor at Graduate School of Engineering, Tokyo Institute of Technology.

Makoto Ando was born in Hokkaido in 1952. He received the doctoral degrees in electrical engineering from Tokyo Institute of Technology in 1979. He is currently a professor emeritus, Tokyo Institute of Technology.

Chapter 1Solutions to Maxwell's wave equations
1.1Radiation from current
1.2Duality of electric and magnetic fields in Maxwell's equations
Chapter 2Equivalence theorem
2.1Uniqueness theorem
2.2Application of the equivalence theorem
2.3Understanding the equivalence theorem
Chapter 3Solutions and features for boundary value problems
3.1Solutions for boundary value problems
3.2Reciprocity theorem
3.3Solving electromagnetic wave scattering problems
Chapter 4Scattering problems in structures conforming to rectangular coordinates
4.1Expressions of complementary solutions in rectangular coordinates
4.2Scattering problem due to a current in a one-end terminated parallel plate conductor
Chapter 5Scattering problems in structures conforming to cylindrical coordinates
5.1Expressions of complementary solutions in cylindrical coordinates
5.2Scattering problem due to an electric current near a cylindrical conductor
5.3Fundamentals of diffraction phenomena
Appendix AVector formulas
Appendix BDelta function
Appendix CFourier integral
Appendix DBessel functions
Appendix EFormulas for diffraction phenomena
References
Index